RAZONES Y PROPORCIONES
Razones y proporciones: Cuando son comparados dos números mediante
una división diremos que esos dos números se encuentran en una razón; y si
igualamos dos razones estamos en presencia de una proporción.
Razón entre números
Al realizar una
encuesta entre los jóvenes entre 18 y 21 años se concluye que: "1 de cada 5
jóvenes está inscrito en el Registro Electoral". Entonces, se puede decir
que la razón entre los que votan y el total de jóvenes es 1: 5. También se
puede decir que la razón entre los que votan y los que no, es 1: 4.
Sean a y b dos números racionales y b ‡ 0,
entonces una razón entre a y b es el cociente a: b = a/b
y lo leeremos a es a b
Como las razones son
números racionales, entonces se puede ampliarla y simplificarla como se desee
mientras se mantenga la razón.
Una de las
situaciones matemáticas más frecuente es sin duda, la de relacionar dos
cantidades: se han hecho al sumarlas y restarlas, o al multiplicarlas y
dividirlas. En particular, al relacionarlas mediante la resta y la división,
estamos comparándolas. Existen dos tipos de comparaciones entre números: las
que nos permiten averiguar cuál es el mayor calculando la diferencia existente
entre ambos, o bien, calculando cuántas veces el mayor contiene al menor. En la
primera situación hablamos de comparaciones o relaciones aditivas y en la
segunda, de relaciones multiplicativas.
El concepto matemático de razón
Una razón es una
relación multiplicativa entre dos números naturales diferentes de 0.
Hablamos así de la
razón “dos a tres”,“1 a 10”, “7 a 4”, etc. Por ejemplo, si en un grupo de
personas hay 18 hombres y 27 mujeres, diremos que la razón entre el número de
hombres y el de mujeres es de “2 a 3”, es decir, que “hay 2 hombres por cada 3
mujeres”. En este caso, la razón entre el número de mujeres y el de hombres es
la inversa, de “3 a 2”, es decir, que “hay 3 mujeres por cada 2 hombres”. Hay
que saber distinguir entre los conceptos de razón y de fracción. Este último
alude a la relación también multiplicativa entre la parte y el todo respectivo.
En el ejemplo anterior, 2/5 representa la fracción ya simplificada
correspondiente al número de hombres (18) con respecto al total de personas
presentes (18 + 27 = 45). En el concepto de razón no está presente esta
relación de carácter parte-todo.
Proporciones
La igualdad entre
dos razones es una proporción.
Se lee:
·
a es a b como c
es a d.
·
También puede
escribirse a: b = c: d
·
En toda proporción
se tiene:
En toda proporción
el producto de los extremos es igual al producto de los medios, esta relación
se conoce como Teorema fundamental de la proporción, es decir.
Un ejemplo de
proporción es 2/3 = 4/6, cuya lectura es “2 es a 3 como 4 es a 6”. De nuevo hay
que recordar la distinción entre razones y fracciones, para no ver en la
expresión anterior “la equivalencia de dos fracciones” (que será la lectura
correcta cuando se hable de fracciones, pero no ahora...).
Vamos con la
nomenclatura relativa a las proporciones. El uso de la notación a : b : :c : d
nos ayuda a identificar a los números a y d como los extremos de la proporción
y a los números b y c como los medios de la proporción. Por ejemplo, en 2/3 =
4/6, 2 y 6 son los extremos de la proporción, y 3 y 4, los medios.
Una proporción cuyos
extremos y medios son diferentes se denomina discreta; por ejemplo, la
anterior. Y continua, si los medios (o los extremos) son iguales entre sí; su
forma sería: a/b = b/c ó a/b = c/a. Por ejemplo, 2/6 =6/18. En una proporción
discreta, cualquier término se denomina cuarta proporcional de los otros tres.
Así, en el ejemplo 2/3 = 4/6 decimos que 3 es cuarta proporcional de 2,4 y 6, ó
que 4 lo es de 2, 3 y 6. En una proporción continua, el término repetido se
denomina media proporcional de los otros dos, y estos dos últimos, tercia
proporcional del otro término. Así, en el ejemplo 2/6 = 6/18, 6 es media
proporcional de 2 y 18, y 2 y 18 son tercias proporcionales de 6.
Videos de Apoyo al tema de Razones y Proporciones
Teorema fundamental de las proporciones
Las proporciones presentan numerosas
propiedades, que ya fueron estudiadas por los griegos y aparecen en el Libro V
de los Elementos de Euclides. Esta es la fundamental: “En toda proporción,
el producto de los medios es igual al producto de los extremos”
Definición de semejanza de triángulos
Videos de Apoyo al tema de Semejanza y Proporciones de Triángulos
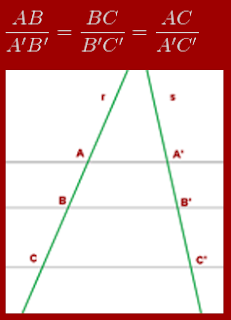
Teorema de Thales
Si dos rectas
cualesquiera se cortan por tres o más rectas paralelas, los segmentos
determinados en una de las rectas son proporcionales a los segmentos
correspondientes en la otra.
Videos de Apoyo al Teorema de Thales
ÁNGULO ALTERNO EXTERNO
Si una recta transversal OP corta a dos rectas paralelas AB y CD,
los ángulos alternos externos son los que están en la parte exterior de
las paralelas a distinto lado de ellas y a distinto lado de la transversal.
ÁNGULO ALTERNO INTERNO
Si una recta transversal OP corta a dos rectas paralelas AB y CD,
los ángulos alternos internos son los que están entre las paralelas a
distinto lado de ellas y a distinto lado de la transversal.
La pareja de ángulos ∡3 y ∡5; ∡4 y ∡6 son congruentes (iguales).
Ángulos correspondientes
Cuando dos líneas se
cruzan con otra (que se llama transversal), los ángulos en las esquinas
correspondientes se llaman ángulos correspondientes.
En este ejemplo, son
ángulos correspondientes:
a y e
b y f
c y g
d y h
Videos de Apoyo a los Ángulos Colaterales












No hay comentarios:
Publicar un comentario